Algorithms

Each algorithm that psimpl provides, is based on a STL-style like interface with input and output iterators that iterate over vertex coordinates, e.g.: x1, y1, z1, x2, y2, z2, ... They all support n-dimensional polylines defined with either floating point or signed integer data types.

For more information about an individual algorithms, click on its name in the sidebar on the left.

The code

psimpl consists of a single header file: psimpl.h. This header file in turn relies only on a handfull of standard C++ headers. No additional libraries or files are needed!

All code in psimpl.h is organized in the following structure:

All the code is contained within the root namespace psimpl. The class scoped_array, similar to boost::scoped_array, is a smart pointer for holding a dynamically allocated array. math is a namespace containing all functions related to computing statistics and squared distances between various geometric entities. The class PolylineSimplification provides the implementation for each simplification algorithm. The top-level functions are for convenience as they provide template type deduction for their corresponding member functions of PolylineSimplification.

psimpl itself does not throw exceptions. The reason for this is that I consider exception handling to be rather rare within C++ applications. Unlike the .NET world, a lot of developers just don't use nor even think about exception handling.

The demo

psimpl demo application screenshot

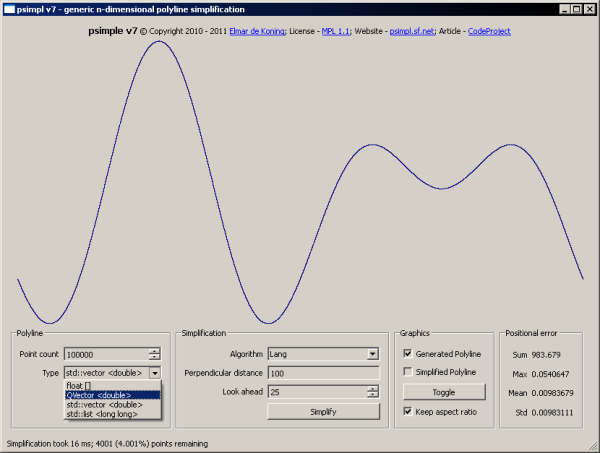
psimpl also provides a 32-bit Windows demo application, that allows you to experiment with the different simplification algorithms. It can generate pseudo random 2D-polylines of up to 10,000,000 vertices in various types of containers. The bounding-box of the generated polyline is always n x n/2, where n is the amount of vertices of the generated polyline. Use this fact to specify a proper tolerances. Comparing the various algorithms can be done visually and by using the computed positional error statistics. These statistics are only available when the value_type of the chosen container is double.

Internally, the generated and simplified polylines are always stored in a QVector<double>. Just before simplification, it is converted to the selected container type. Afterwards, this temporary container is destructed. Normally, you won't notice this, but it seems that creating and destructing a std::list(10.000.000) can take a rather long time. The resulting performance measurements never include these conversion steps. I chose this approach as it allowed me to quickly add new container types.

Note that the entire application is single threaded (sorry for being lazy), meaning it could go 'not responding' during a long-running simplification.

The demo application was made using Qt 4.7.3, Qt Creator 2.1.0, and Visual Studio 2008 Express. Complete source code is included.

Upcomming versions

The following algorithms are planned for upcomming versions:


Other things that I want to look into include: