Perpendicular Distance
Instead of using a point-to-point (radial) distance tolerance as a rejection criterion (see Radial Distance), the O(n) Perpendicular Distance routine uses a point-to-segment distance tolerance. For each vertex vi, its perpendicular distance to the line segment S(vi-1, vi+1) is computed. All vertices whose distance is smaller than the given tolerance will be removed. This process is illustrated below:
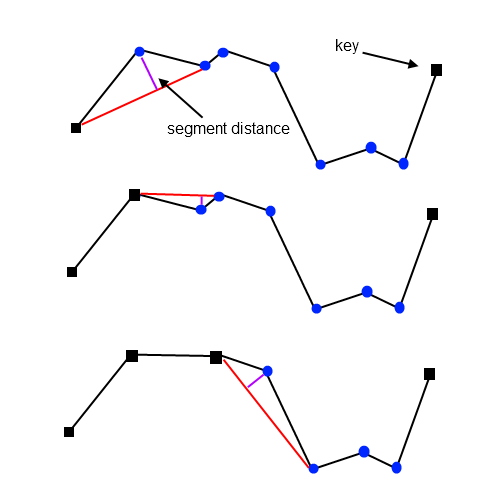
Initially, the first three vertices are processed, and the perpendicular distance of the second vertex is calculated. After comparing this distance against the tolerance, the second vertex is considered to be a key (part of the simplification). The algorithm then moves one vertex up the polyline and begins processing the next set of three vertices. This time, the calculated distance falls below the tolerance and thus the intermediate vertex is removed. The algorithm continues by moving two vertices up the polyline.
Note that for each vertex vi that is removed, the next possible candidate for removal is vi+2. This means that the original polyline can only be reduced by a maximum of 50%. Multiple passes are required to achieve higher vertex reduction rates.
Interface
template <unsigned DIM, class ForwardIterator, class OutputIterator> OutputIterator simplify_perpendicular_distance ( ForwardIterator first, ForwardIterator last, typename std::iterator_traits <ForwardIterator>::value_type tol, OutputIterator result) template <unsigned DIM, class ForwardIterator, class OutputIterator> OutputIterator simplify_perpendicular_distance ( ForwardIterator first, ForwardIterator last, typename std::iterator_traits <ForwardIterator>::value_type tol, unsigned repeat, OutputIterator result)
Applies the Perpendicular Distance routine
(repeat times) to the range [first, last) using the
specified perpendicular distance tolerance tol. The resulting
simplified polyline is copied to the output range [result, result + m * DIM),
where m is the number of vertices of the simplified polyline. The
return value is the end of the output range: result + m * DIM.
Input (Type) Requirements
DIMis not 0, whereDIMrepresents the dimension of the polyline- The
ForwardIteratorvalue type is convertible to the value type of theOutputIterator - The range
[first, last)contains vertex coordinates in multiples ofDIM, e.g.: x, y, z, x, y, z, x, y, z whenDIM= 3 - The range
[first, last)contains at least 2 vertices tolis not 0nis not 0
In case these requirements are not met, the entire input range
[first, last) is copied to the output range
[result, result + (last - first)), or compile errors may
occur.
Implementation Details
The main function, without the repeat parameter, is a single loop
that starts with processing the first three consecutive vertices. Depending on
whether the second or third vertex is considered to be part of the simplification
(called a key), the algorithm moves one or two vertices up the original polyline.
As soon as a key is found, it is copied to the output iterator.
The second function, which takes a repeat value as input, is a
wrapper around the main function, and consists of three distinct steps:
- First iteration: simplify from range
[first, last)to a plain C-style array. - Intermediate iterations: simplify from and to plain C-style arrays.
- Last iteration: simplify from a plain C-style array to the output iterator
result.
After each iteration, the simplification is checked for improvement. If none
was found, the current result is copied directly to the output iterator
result. Note that up to two temporary copies may be created: one
copy of the input range, and the other of the first intermediate simplification
result.
Usage
double tolerance = 10.0; // point-to-segment distance tolerance std::deque <double> polyline; // original polyline, assume not empty std::deque <double> result; // resulting simplified polyline // simplify the 3d polyline - single pass psimpl::simplify_perpendicular_distance <3> ( polyline.begin (), polyline.end (), tolerance, std::back_inserter (result)); double tolerance = 10.0; // point-to-segment distance tolerance usinged repeat = 5; // apply the routine 5 times std::deque <double> polyline; // original polyline, assume not empty std::deque <double> result; // resulting simplified polyline // simplify the 3d polyline - multi pass psimpl::simplify_perpendicular_distance <3> ( polyline.begin (), polyline.end (), tolerance, repeat, std::back_inserter (result));